Research group of Prof. Jian-Wen Dong and Prof. Wen-Jie Chen achieved new progress in topological photonic crystals

As we all know, the realization of new optical field manipulation can reveal fundamental optics and find new applications, which has a wide range of application prospects in the fields of information, life, chemistry and materials. In recent years, topology has been introduced into photonics, and a variety of nontrivial photonic topological insulators have been discovered. They have realized some fancy phenomena such as unidirectional light propagation and backscattering immune transmission, and designed high-performance photonic waveguides and microcavities. Among different photonic systems, photonic crystals have become one of the most important systems for studying topological physics because of their flexible and adjustable photonic bands. In order to realize topological photonic crystals, it is necessary to design the crystal configuration and the material parameters carefully. For example, Hall typed topological photonic crystals need to be realized by applying external magnetic fields to magnetic materials, and spin-Hall typed topological photonic crystals need to be realized by designing complex metamaterials. This not only increases the difficulty of design, but also results in topological devices with different morphologies, which is difficult to cascade. Therefore, it is not only an important scientific issue to realize nontrivial topological structures from arbitrary periodic structure, but also an important step to make topological devices move from theory to application.

To solve this problem, Professor Jian-Wen Dong and Prof Wen-Jie Chen from the School of Physics at Sun Yat-sen University reviewed the existing work in higher dimensional space and found that people used to realize topological photonic crystals in momentum space. However, the dimension of momentum space is generally consistent with that of real space, which greatly hindered the exploration of topological modes in high dimensional space. Inspired by synthetic dimension and four-dimensional quantum Hall effect, they constructed a second Chern crystal in four-dimensional space by introducing two additional synthetic translation dimensions and combining two momentum dimensions (Figure 1(a)). Different from the first Chern number in two-dimensional space, the second Chern number is the topological invariant that characterizes the topological properties of crystals in four-dimensional space. Through rigorous derivation and detailed numerical calculation, they found that the second Chern number of each independent band in the four-dimensional abstract space is identical to 1, which confirms the intrinsic nontrivial topological property of this second Chern crystal. Furthermore, the localized boundary modes can be obtained when the second Chern crystal is truncated. In particular, when dimensionality truncation is carried out with PEC boundary in both x and y directions, gapless localized corner modes can be observed (Figures 1(b)&1(c)). Note that the existence of this gapless corner modes does not depend on crystal symmetry, and thus provides a generalized scheme to achieve localized modes in arbitrary crystal structure. In addition, the frequency of corner modes covers the whole band gap, which is also important for the flexible design of topological photonic devices. On the other hand, dislocation is a common real space crystal defect, which can also support localized modes. By projecting a four-dimensional space into a one-dimensional space through dimensional reduction, a one-dimensional topological dislocation mode is found. Specifically, after fixing the transverse translation Δx for each cylinder in the unit cell, and establishing the linear relationship between the longitudinal translation Δy and the azimuth angle θ, the dislocation characterized by the Burgers vector can be obtained, which can realize localized modes without relying on the PEC boundary (Figure 1(d)). Furthermore, the topological dislocation mode can construct a one-dimensional vortex pattern after considering all possible Δx (Figure 1(e)). In particular, this topological dislocation mode dispersion persists even after the introduction of additional defects, proving its robustness (Figures 1(f)&1(g)).

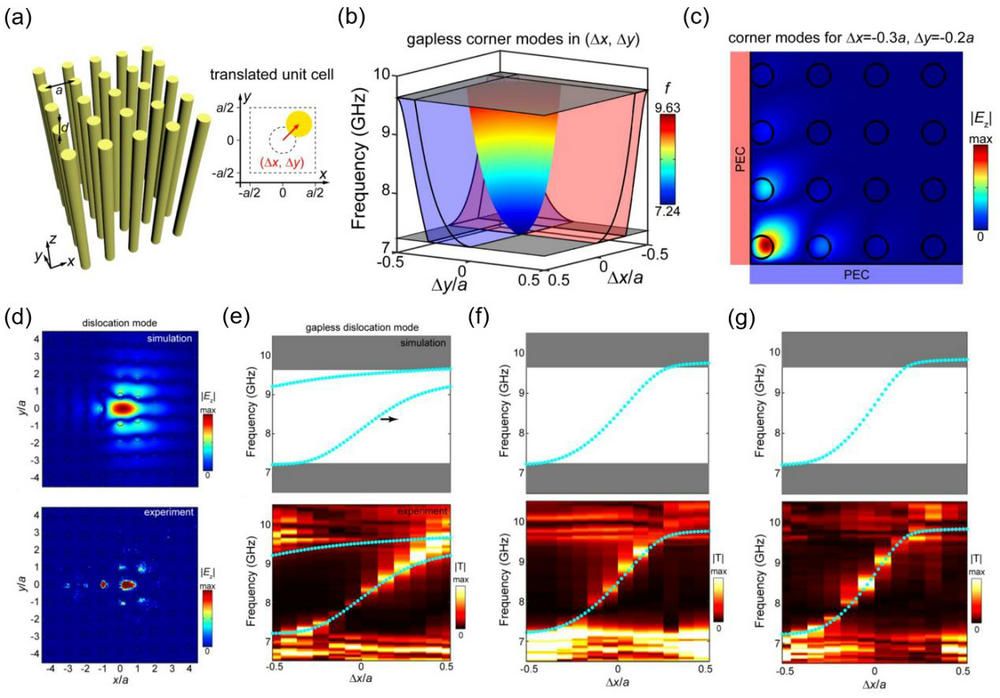
Figure 1. (a) Schematic of the second Chern crystals within synthetic translation dimension. (b&c) Band dispersion and field pattern of localized corner modes. (d) Simulated and measured |Ez| fields of dislocation mode. (e-g) Band dispersion of gapless dislocation modes with (e) no disturbance, (f) an additional dielectric rod and (g) and inserting perfect electric conductor.

This work is published in National Science Review entitled “Second Chern crystals with inherently nontrivial topology”. Associate Professor Xiao-Dong Chen is the first author. Prof. Jian-Wen Dong and Prof. Wen-Jie Chen are corresponding authors. Prof. C. T. Chan from HKUST make important contributions in this research. This study was supported by National Natural Science Foundation of China, Guangdong Basic and Applied Basic Research Foundation, etc. Also, the School of Physics and the State Key Laboratory of Optoelectronic Materials and Technologies gave significant support to this work.

Link to the paper: https://doi.org/10.1093/nsr/nwac289