
拓扑物相的主要特征为能隙间存在受体拓扑保护的边界态,这类物态通常由定义在整个布里渊区内的拓扑不变量刻画。近年来,一类新型的高阶拓扑相受到广泛关注,其中,具有n阶拓扑性质的d维系统,其拓扑边界态局域在系统的(d-n)维边界上。与传统拓扑相相比,“边界的边界”拓扑态可能同时涉及到系统体态及低维边界态的拓扑性质,具有更丰富的体边对应关系及拓扑分类。但目前,对高阶拓扑相的拓扑刻画大都依赖于具体模型的空间对称性,仍缺乏一个可直接通过实验探测的普适性拓扑刻画理论。
近日,我校物理与天文学院量子工程与精密测量团队李林虎副教授与新加坡国立大学的龚江滨教授及朱伟伟博士合作,针对复对称类高阶拓扑相,提出了一套基于动力学的嵌套拓扑刻画理论。该理论基于系统动量空间哈密顿量定义了一系列互相嵌套的“能带反转面”(band inversion surfaces),系统整体的高阶拓扑性质由这些能带反转面分别对应的拓扑不变量及相互嵌套关系决定(见图1)。特别的,通过这种方式定义的拓扑不变量,可直接由系统赝自旋纹理的卷绕性质给出,并可通过量子淬火动力学中系统的长时间演化进行测量。同时,这套高阶拓扑刻画方案不依赖于系统的空间对称性,适用于满足克利福德代数(Clifford algebra)的任意高阶拓扑相。这项工作将不受空间对称性保护的高阶拓扑相这一概念,拓展到了任意维度任意拓扑阶数的一整类高阶拓扑相,并提出了一套普适的拓扑刻画理论,极大地加深了对高阶拓扑相的认识。此外,该工作所提出的拓扑刻画方案亦可以在超冷原子及固态量子比特等多种量子模拟平台中通过动力学性质来测量,为实验上研究高阶拓扑相提供了便利。
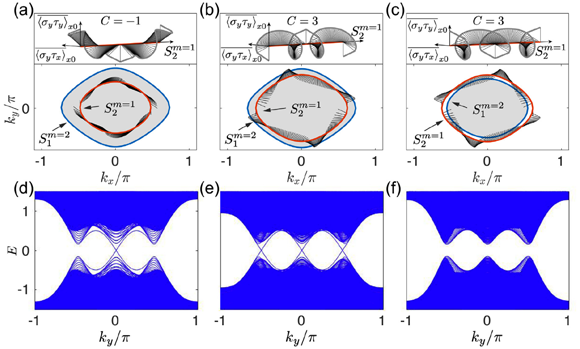
图1:当系统的能带反转面按顺序嵌套时(a,b),系统中存在类手征高阶拓扑边界态(d,e),其数量由不同能带反转面上赝自旋卷绕数确定。当能带反转面不按顺序嵌套时(c),系统不存在高阶拓扑边界态(f)。
该成果以“Direct dynamical characterization of higher-order topological phases with nested band inversion surfaces”为题在线发表在中科院一区期刊Science Bulletin上,李林虎副教授为第一作者,新加坡国立大学龚江滨教授为通讯作者。该研究得到了广东省量子精密测量与传感重点实验室的大力支持。