
心理学系潘俊豪副教授等通过把机器学习中Lasso (Least Absolute Shrinkage and Selection Operator )正则化算法和心理学领域的经典模型验证性因素分析模型(Confirmatory Factor Analysis,CFA)结合,成功建立了带局部项目依赖的CFA模型,在贝叶斯方法的框架下,对项目测量误差之间的协方差使用双指数先验分布(如下图),解决了在运用CFA模型分析心理学实际数据过程中数据出现违反“局部独立性”假设时应如何建模的问题。 该研究近日发表于心理学顶级期刊《心理学方法》(Psychological Methods)。
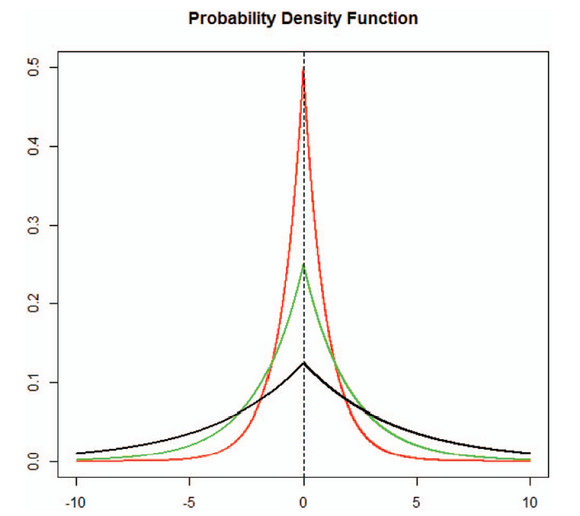
不同收缩参数下双指数分布的概率密度函数
验证性因素分析模型广泛应用于心理学、社会学等领域的科学研究当中,以研究指标变量(Indicator)和潜变量(Latent Variable)之间的关系。在建模过程中,CFA模型(以及其他潜变量模型)的一个重要前提假设是局部独立性(Local Independence),违反局部独立性假设的情况称为局部项目依赖。在实际数据分析当中,研究者往往默认局部独立性假设成立从而建立测量模型。然而,随着研究的深入,研究者逐渐意识到错误地假设局部独立性会对研究结果(特别是估算潜变量之间的关系)产生严重的误导。作为最基础的潜变量模型之一,在CFA模型的统计分析中如何有效地考虑指标变量间的局部依赖程度并研究相应的统计分析方法一直是学界关注的热点问题。此问题的解决将有助于解决其他潜变量模型中不满足局部独立性时应如何建模的问题。潘俊豪副教授等的研究成果为此提供了新的研究思路。
《心理学方法》(Psychological Methods)时任副主编宾夕法尼亚州立大学Sy-Miin Chow教授认为该成果“能为CFA模型的研究做出有价值的贡献(a valuable contribution)”;其他匿名评审者认为“把贝叶斯Lasso先验应用于CFA建模是一个伟大的想法(a very great idea)”,“解决了CFA使用过程中一个重要的问题(an important issue)”。
《心理学方法》(Psychological Methods)由美国心理学会出版,是心理学,特别是心理学研究方法领域顶级期刊,SSCI收录,2016年影响因子4.667,5年影响因子10.141。据悉,这是心理学系教师在该刊发表的第一篇第一作者论文,也是第二篇大陆高校学者第一作者论文。
文章来源:
Pan, J., Ip, E. H., & Dubé, L. (2017). An alternative to post hoc model modification in confirmatory factor analysis: The Bayesian lasso. Psychological Methods, 22(4), 687-704. http://dx.doi.org/10.1037/met0000112